Sep 1

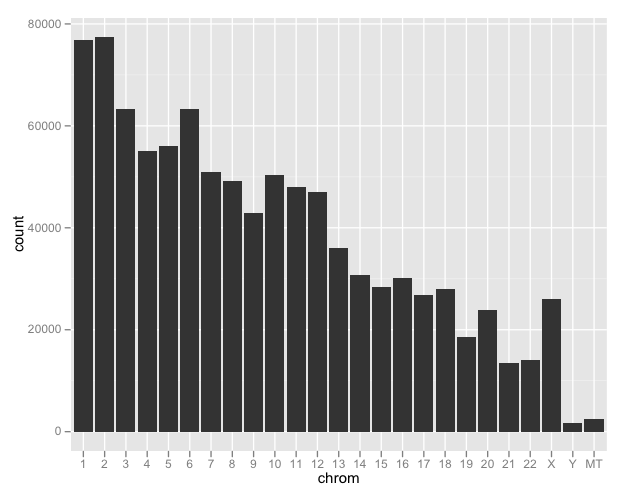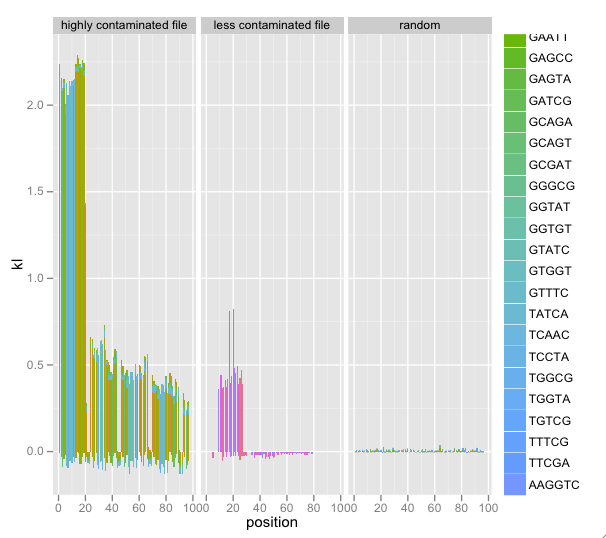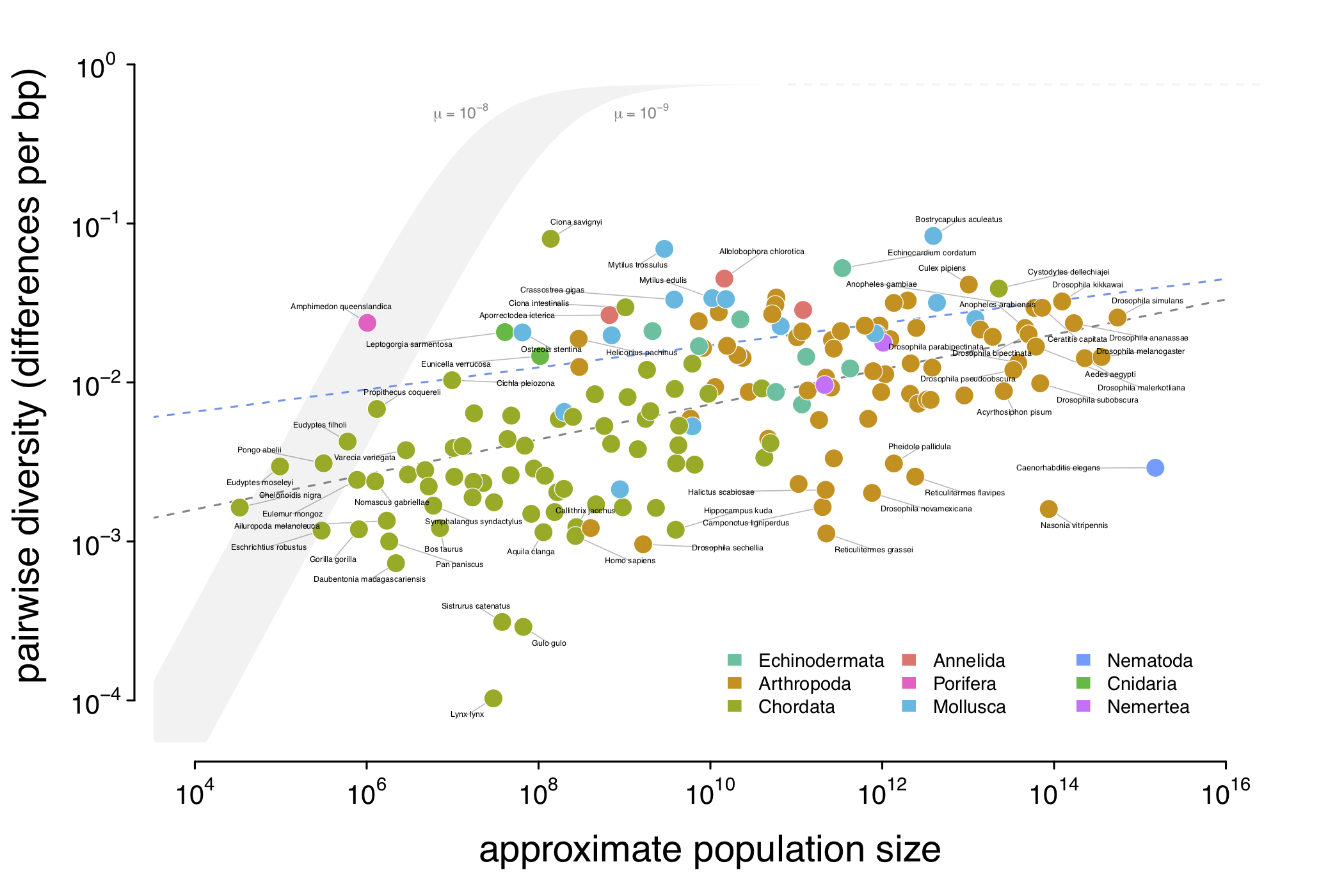
Why Do Species Get a Thin Slice of π? Revisiting Lewontin's Paradox of Variation

The Great Obsession of population geneticists, to borrow John Gillespie's words, is genetic variation. As an evolutionary biologist, it's rather hard to not be obsessed with genetic variation, for it's the ultimate source of the two most striking features of life on earth: the mind-boggling diversity of species, and adaptations so utterly clever they look as though they were assembled by a designer. Both life's dizzying diversity and cunning adaptations are the result of evolutionary processes like natural selection and numerous historical accidents, overlaid on one another...

Aug 20

The Problem of Detecting Polygenic Selection from Temporal Data

Darwin thought natural selection was slow, but we now know it can act rapidly. The challenge is detecting this selection at the DNA level—especially when adaptation involves many genes of small effect acting in concert.

Aug 20

The Genome-wide Signal of Linked Selection in Temporal Data

The last chapter of my dissertation with Graham Coop was recently published in PNAS last week. In an effort to communicate my research to a broader audience, I have written two blog posts on our work. The first post, is meant to introduce the historical context and concepts like linked selection and polygenic adaptation to a non-scientist, and the second post, below, describes our work on temporal covariance as a signature of polygenic linked selection and its application to four evolve-and-reseqeunce data sets.

Mar 4

Understanding Snakemake

Snakemake automates the tedious task of re-running data processing pipelines when upstream files change. This tutorial explains how Snakemake works by first covering its predecessor, Make, and the core idea of dependency graphs.

Apr 3

A Genealogical Look at Shared Ancestry on the X Chromosome

The X chromosome has a peculiar inheritance pattern: it's passed from mothers to all children, but fathers only pass it to daughters. This creates an embedded genealogy of X ancestors that affects how segments of DNA are shared between relatives.

Dec 5

Using Rcpp and C++ to Count Genotypes

R's apply and table functions are flexible but slow for counting genotypes in large matrices. A simple Rcpp function provides a 10x speedup by specializing for the 0/1/2/NA genotype encoding.

Jan 17

MD Tags in BAM Files

The MD tag in BAM files encodes information about the reference sequence at aligned positions, allowing SNP and indel calling without the reference. These notes work through several examples of how MD tags interact with CIGAR strings.

Aug 8

Using Named Pipes and Process Substitution in Bioinformatics

Unix pipes are elegant, but they don't work when programs have multiple inputs or outputs. Named pipes and process substitution solve this problem, and the performance gains over writing intermediate files to disk are substantial.

Jan 26

Bioinformatics and Interface Design

Bioinformatics involves a tremendous amount of interfacing between programs, yet this receives surprisingly little design attention. Better interfaces—through foreign function interfaces, shared libraries, and cleaner design patterns—could save us from the current mess of file parsing and system calls.

Jan 13

21st Century Science and the Need for Open Data and Open Tools

Science is increasingly data-driven, yet there's a troubling asymmetry in how we're taught to handle data versus how we actually should. The rise of open data offers tremendous opportunities, but realizing its potential requires rethinking how we train scientists.

Nov 14

My First Recommendation to New Scientific Coders: Learn Visualization

If you can visualize data quickly, problems look different. Learning to make plots without friction means you'll use visualization as a debugging tool, catch confounders early, and notice mistakes that would otherwise go undetected.

Oct 8

Simple Parallel Bioinformatics Pipelines with find, basename, and xargs

A practical design pattern for parallelizing bioinformatics file processing using find, basename, and xargs. This approach scales well for data-parallel tasks across multiple cores on a single server.

Mar 12

Using Bioconductor to Analyze your 23andme Data

A tutorial on loading 23andme genotype data into R and using Bioconductor's gwascat and GenomicRanges packages to explore GWAS associations, find SNPs in genes like APOE, and visualize risk alleles.

Mar 11

Git Notes

Notes on Git internals and workflows, covering remote tracking branches, the relationship between fetch and pull, and common use cases with illustrative examples.

Mar 8

The Beauty of Bioconductor

Bioconductor solves several hard problems in reproducible bioinformatics: versioned software, packaged data, and strict coding standards. As genomics data grows, these problems will only get worse—Bioconductor offers a way forward.

Mar 7

Thoughts on Julia and R

Julia is a fast, promising new language for technical computing. But challenging R means replicating not just the language, but the entire ecosystem of CRAN and Bioconductor packages—a massive undertaking.

Mar 3

The Unbelievable Debate: Some Ramblings on Machine Learning in Science

Machine learning is powerful, but it's easy to let its pattern-finding abilities bias our understanding of complex systems. Coming from the social sciences, where data mining was frowned upon, I've had to recalibrate—but the old caution about confusing prediction with understanding still holds.

Mar 1

Elucidating k-mer Contamination with Kullback-Leibler Divergence

When sequencing data is severely contaminated, finding the culprit can be tricky. Using k-mer frequency analysis and Kullback-Leibler divergence, we can identify contamination patterns that would otherwise be invisible.

Feb 21

Please developers, don't be dicks.

Open source software benefits from a large, diverse user base, but this growth brings growing pains. Being rude to users doesn't help anyone—it hurts OSS adoption, poisons collaboration, and ultimately damages science.