The Problem of Detecting Polygenic Selection from Temporal Data
The last chapter of my dissertation with Graham Coop was recently published in PNAS (pdf, bioRxiv) last week. In an effort to communicate my research to a broader audience, I have written two blog posts on our work. The first post, below, is meant to introduce the historical context and concepts like linked selection and polygenic adaptation to a non-scientist, and the second post describes our work on temporal covariance as a signature of polygenic linked selection and its application to four evolve-and-reseqeunce data sets.
Natural Selection is Rapid
For nearly seventy years, we have known Charles Darwin was wrong about a key aspect of natural selection: that it was slow acting. In the first edition of The Origin of Species, Darwin wrote of natural selection,
We see nothing of these slow changes in progress, until the hand of time has marked the long lapse of ages, and then so imperfect is our view into long past geological ages, that we only see that the forms of life are now different from what they formerly were.
While Darwin knew artificial selection1 could rapidly change an organism’s traits, it was only until ecological geneticists E.B. Ford and Bernard Kettlewell showed rapid changes in moth wing coloration, that it was recognized that natural selection could act over very short timescales. Since, evolutionary biologists have shown rapid adaptation is remarkably common in a variety of species including sticklebacks2, Anolis lizards3, soapberry bugs4, guppies5, and field mustard6.
Natural Selection versus Drift
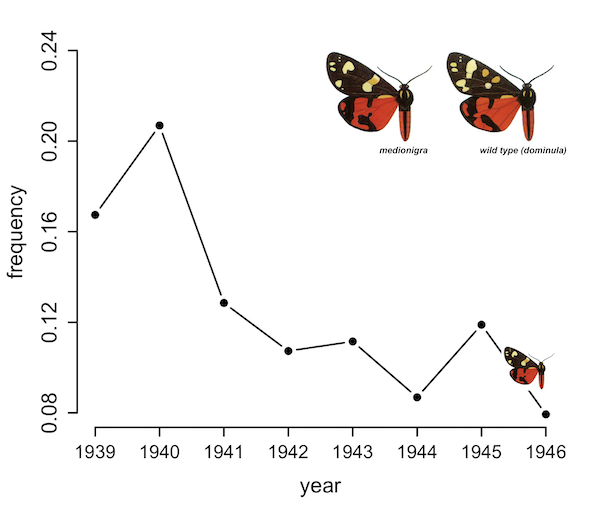
observed in Oxford by Fisher and Ford (1947).
In one classic study, E.B. Ford and R.A. Fisher tracked the frequency of dark wing color variant in a population of scarlet tiger moths around Oxford for nearly a decade. The dark wing variant declined quickly in frequency (see figure above), which they believed was caused by natural selection against this variant. However, to demonstrate that natural selection drove this change, they had to rule out another possible explanation: genetic drift. Genetic drift is another factor that leads the frequency of alleles7 in populations to vary through time, caused by random chance. Some individuals in a population may get lucky, and encounter an abundance of resources that allow them to leave more offspring; some may experience random hardships that force them to leave fewer. Unlike with natural selection, the underlying causes of variation in survival and family size due to drift are not genetic, but random; consequently they are not inherited by the next generation. Another major source of randomness is Mendelian segregation: if you carry two different copies of a gene (one you inherited from your father, one you inherited from your mother), the copy you pass to your child is determined essentially by a biological coin flip.
These random changes in allele frequency across families lead to a random behavior of allele frequencies within a population, which could, purely by chance, also lead to the decline of a particular wing coloration through time that Ford observed. To discern natural selection from random drift, Ford collaborated with R.A. Fisher, who developed a statistical method that used population size estimates to determine the strength of genetic drift (genetic drift is the strongest in small populations, where a single family’s reproductive fortunes have a larger proportional impact). Their 1947 paper argued the change in the frequency of the dark wing variant through time was caused by natural selection, not genetic drift; this later lead to a vitriolic debate between Ford and Fisher and Sewall Wright, the leading proponent of genetic drift at the time.
We can study natural selection through its effects on linked sites
Since this early work using temporal data, there was a relative lull as efforts shifted towards detecting selection from single present-day population genetic samples, until the tremendous growth in DNA sequencing technology over the last two decades. Now, researchers can directly observe allele frequency changes through time all across an organism’s genome (millions of sites), rather than at a few sites that affect traits (e.g. darker wing color). This has spurred the further development of statistical methods that can differentiate allele frequency changes caused by selection from those caused by random drift8. Simultaneously, new statistical methods were discovering the footprints left by natural selection in our DNA and the DNA of many other species, by the effect selection has on its neighboring sites.
When a new beneficial mutation arises in a population, its comparative advantage (either through increasing survival or in leaving more offspring) causes it to quickly rise in frequency. Alleles reside on our chromosomes, and are linked, or coupled to their neighbors because large contiguous stretches of our chromosomes are inherited together. A process known as recombination does shuffle up chromosomes a bit, since each chromosome we inherit from our father is a patchwork of our paternal grandparent’s chromosomes (and likewise with our maternal chromosomes). Consequently, when beneficial mutations rise in frequency, they drag along neighboring alleles that happen to be lucky enough to reside upon the same chromosome that the beneficial mutation arose (we call this “genetic hitchhiking”9 since these alleles hitch a ride along with the beneficial mutation). We can detect these events because they wipe out genetic variation in spots along the genome, since, in essence, everyone derives their ancestry in this region from the individual in which the beneficial mutation first arose.
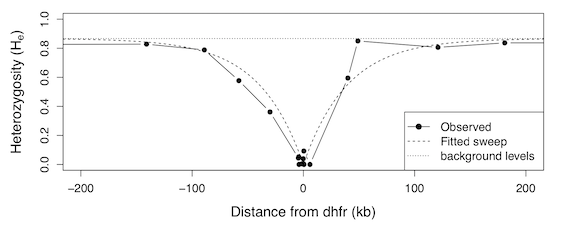
Data from Nash et al. (2005), figure produced by Graham Coop in his population genetics notes.
One remarkable finding of the last three decades was that mutations that are disadvantageous, or deleterious (that is, they leave fewer offspring or lower odds of survival) also extinguish genetic variation in a region. This effect is known as background selection. Collectively, the hitchhiking effect and background selection are types of linked selection, and this is a primary focus of Graham and my work. There is a great deal of mathematical theory that predicts the extent to which, and over how long a stretch of chromosome, genetic variation is wiped out by genetic hitchhiking and background selection. From this body of work, we predict regions of high recombination (i.e. an allele is very likely to be randomly shuffled off its chromosome background) reduce linked selection’s effects on genetic variation, while in regions of low recombination (i.e. an allele is very unlikely to be shuffled off its chromosome background) are drastically affected by linked selection. These predictions have been confirmed in numerous studies, perhaps most famously by Begun and Aquadro (1992) in the fruit fly Drosophila melanogaster, where they find a strong correlation between the amount of recombination and the level of pairwise diversity, a common measure of genetic variability.
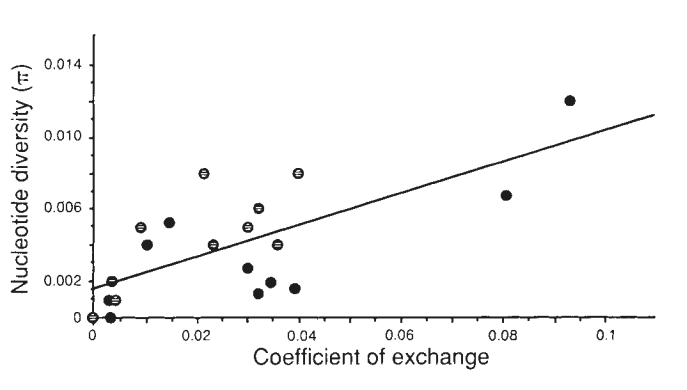
in Drosophila melanogaster, from Begun and Aquadro (1992).
Over the last fifty years, we have come to recognize that linked selection itself introduces a source of randomness, much like genetic drift, into evolution; we call this genetic draft. Since new selected mutations (whether advantageous or injurious) arise on random chromosomes in the population, and since recombination randomly shuffles these chromosomes through the generations, an allele’s frequency may jiggle about through time not only due to genetic drift, but by the fitness of whatever background it happens to find itself on. Our understanding of evolutionary genetics will not be complete until we can differentiate between the randomness of genetic drift from the randomness of linked selection. This open problem is reminiscent of the same debates that Fisher and Ford were having over seventy years ago.
The Problem of Polygenic Selection

Image from Schilling et al. (2012).
Over the last decade, modern genomic data sets have advanced the field of quantitative genetics as well. Quantitative genetics studies the nature of continuous traits, such as height, including how selection operates on these traits and how variability for these traits arises in populations. One of the triumphs of the Modern Synthesis10 was finding that the same Mendelian genetic system that determines discrete traits, like wing coloration, also determines continuous traits like height. The difference is that while a single gene may determine wing coloration, hundreds to thousands of genes each have a small effect on height; such traits are known as polygenic traits. These small differences across numerous genes, as well as environmental factors, add up to determine one’s height; across a population, the genetic differences between individuals lead to a smooth distribution of traits that looks normally distributed (i.e. having a bell curve shape, such as the distribution of heights pictured above).
Selection also acts on continuous traits, which has enabled humans to continually increase crop yields, breed cows that produce more milk, and so forth. Like population genetics, a rich body of mathematical theory can predict the response to selection and many other aspects of quantitative traits. However, unlike population genetics theory, the mathematical theory of quantitative genetics does not concern itself with the allele frequency changes at each of the sites that determine a trait’s value, but rather takes a macroscopic approach that focuses on a trait’s mean and variance, much like the macroscopic view of the ideal gas law in physics. Bridging this macroscopic quantitative genetics view with the microscopic population genetics view of individual genes has proved to be an arduous task for many reasons.
One key difficulty is that when a polygenic trait like height is selected for, the effects of selection are distributed across all the hundreds or thousands of sites that contribute to the trait’s value. Consequently, the effect of selection at any one site is minuscule, and its frequency trajectory through time will not look like the rapid change in frequency that Fisher and Ford saw with wing coloration in scarlet tiger moths. Worse, such small changes in allele frequency change can easily be mistaken for the random changes caused by drift.
In sum, evolutionary geneticists are left with an interesting quandary. We can readily observe rapid adaptation in natural populations, as traits change through time to better suit a new environment. Yet, despite the present abundance of population genomic data, it can be difficult to detect selection on polygenic traits from temporal data at the DNA level, since the allele frequency changes are minor and hard to differentiate from random genetic drift. Furthermore, since these allele frequency changes are seemingly indistinguishable from genetic drift, even with temporal data we are not able to discern what fraction of allele frequency changes are due to drift, and what fraction are due to selection. These are the problems my work with Graham Coop is working to address.